Last Updated on July 23, 2023
Short Answer
To find the area of a triangle with two sides of lengths 5 and 13, we can use the formula for the area of a triangle: A = 1/2 * base * height. In this case, the two given sides can be considered as the base and height of the triangle. So, the area would be A = 1/2 * 5 * 13 = 32.5 square units.
Understanding the importance of finding the area of a triangle with given side lengths is a fundamental concept in geometry. Whether you’re a student studying for a math exam or a professional in a field that requires geometric calculations, knowing how to find the area of a triangle is essential. In this article, we will explore the formula for calculating the area of a triangle and provide a step-by-step guide to finding the area of a triangle with two sides measuring 5 and 1We will also discuss the concept of a base and height in triangle calculations, and how to determine the length of the base and the height using the given side lengths. Additionally, we will delve into real-life applications of finding the area of a triangle and provide tips and tricks for efficiently calculating it. By the end of this article, you will have mastered the art of finding the area of a triangle with two sides of lengths 5 and 13.
Exploring the formula for calculating the area of a triangle
Calculating the area of a triangle is an essential skill in geometry. It allows us to determine the amount of space enclosed within the triangle’s boundaries. One common method for finding the area of a triangle is by using the formula: Area = 1/2 * base * height. This formula applies to all types of triangles, regardless of their shape or size.
- The base of a triangle is any one of its sides, while the height is the perpendicular distance from the base to the opposite vertex.
- By knowing the lengths of two sides of a triangle, we can determine the length of the base and the height, which are necessary for calculating the area.
- The Pythagorean theorem is often used to find the height of a triangle when only the lengths of two sides are given.
- Once we have the base and height, we can plug them into the formula to find the area of the triangle.
Understanding and applying this formula is crucial for various real-life applications, such as architecture, engineering, and design. By mastering the art of finding the area of a triangle, we can solve complex problems and make accurate measurements in these fields.
Step-by-step guide to finding the area of a triangle with two sides measuring 5 and 13
Calculating the area of a triangle can seem daunting, but with the right formula and a step-by-step approach, it becomes much simpler. In this guide, we will walk you through the process of finding the area of a triangle with two sides measuring 5 and 13.
Understanding the concept of a base and height in triangle calculations
Before we dive into the calculations, it’s important to understand the concept of a base and height in triangle calculations. The base of a triangle is one of its sides, while the height is the perpendicular distance from the base to the opposite vertex.
Calculating the length of the base using the given side lengths
To find the length of the base, we need to determine which side of the triangle is the base. In this case, we are given two sides measuring 5 and 1The base will be the side that is not 1Therefore, the length of the base is 5.
Determining the height of the triangle using the Pythagorean theorem
Next, we need to find the height of the triangle. We can use the Pythagorean theorem to do this. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Understanding the concept of a base and height in triangle calculations
When it comes to calculating the area of a triangle, understanding the concept of a base and height is crucial. The base of a triangle is simply one of its sides, while the height is the perpendicular distance from the base to the opposite vertex. These two measurements are essential in determining the area of a triangle.
To visualize this, imagine a triangle with two sides measuring 5 and 1The base of this triangle would be the side measuring 5 units, while the height would be the perpendicular distance from the base to the opposite vertex. By knowing the base and height, we can use a simple formula to calculate the area of the triangle.
It’s important to note that the base and height of a triangle can be any two sides, as long as they are perpendicular to each other. This means that even if the given side lengths are different from 5 and 13, the concept of base and height remains the same.
Calculating the length of the base using the given side lengths
Before we can calculate the area of a triangle, we need to determine the length of the base. The base of a triangle is one of its sides, and in this case, we are given two sides measuring 5 and 13 units.
- To find the length of the base, we need to identify which side is the base. In a triangle, the base is usually the side that is perpendicular to the height.
- Using the given side lengths, we can determine that the side measuring 13 units is the base.
Now that we have identified the base, we can move on to finding the height of the triangle.
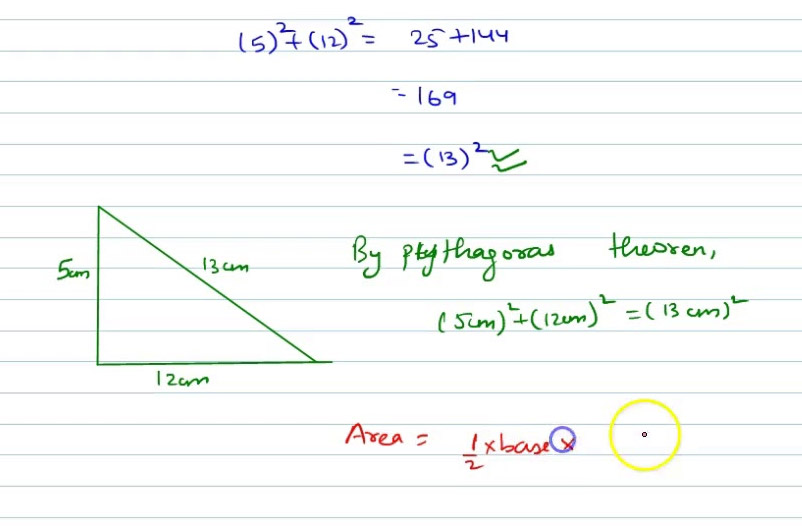
Determining the height of the triangle using the Pythagorean theorem
Once we have calculated the length of the base, the next step is to determine the height of the triangle. The height is the perpendicular distance from the base to the opposite vertex. We can use the Pythagorean theorem to find the height.
- The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
- In our case, the base of the triangle is one of the sides, and the height is the other side. The hypotenuse is the side with length 13.
- We can set up the equation as follows: base^2 + height^2 = hypotenuse^2.
- Substituting the values we know, we get: 5^2 + height^2 = 13^2.
- Simplifying the equation, we have: 25 + height^2 = 169.
- By subtracting 25 from both sides, we find: height^2 = 144.
- Taking the square root of both sides, we get: height = 12.
Therefore, the height of the triangle is 12 units.
Applying the formula for finding the area of a triangle using the base and height
Now that we have determined the base and height of the triangle, we can apply the formula for finding its area. The formula for calculating the area of a triangle is: Area = (base * height) / 2.
In our case, the base of the triangle is 5 units and the height is 12 units. Plugging these values into the formula, we get: Area = (5 * 12) / 2 = 30.
Therefore, the area of the triangle with side lengths of 5 and 13 is 30 square units. It is important to note that the area of a triangle is always measured in square units because it represents the amount of space enclosed by the triangle.
By applying this formula, we can find the area of any triangle as long as we know the lengths of its base and height. This knowledge can be useful in various real-life applications, such as calculating the area of land or determining the size of a triangular-shaped object.
Exploring real-life applications of finding the area of a triangle with given side lengths
Understanding how to find the area of a triangle with given side lengths is not only a valuable mathematical skill, but it also has numerous real-life applications. One common application is in the field of architecture and construction. Architects often need to calculate the area of triangular surfaces, such as roofs or facades, to determine the amount of materials needed for construction.
Another practical application is in the field of land surveying. Surveyors use the concept of finding the area of a triangle to measure the size of irregularly shaped plots of land. By measuring the lengths of two sides and the angle between them, surveyors can accurately calculate the area of the land.
Furthermore, the concept of finding the area of a triangle is also used in various engineering disciplines. For example, civil engineers use this knowledge to design bridges and determine the load-bearing capacity of triangular support structures.
Overall, understanding how to find the area of a triangle with given side lengths is not only a fundamental mathematical concept, but it also has practical applications in various fields, making it a valuable skill to possess.
Tips and tricks for efficiently calculating the area of a triangle
Calculating the area of a triangle can sometimes be a challenging task, especially when you are given specific side lengths. However, with a few tips and tricks, you can efficiently solve this problem.
1. Use the formula: The formula for finding the area of a triangle is (base * height) / 2. By plugging in the values of the base and height, you can easily calculate the area.
2. Remember the Pythagorean theorem: If you are given two sides of a triangle, you can use the Pythagorean theorem to find the length of the third side. This will help you determine the height of the triangle, which is crucial for calculating the area.
Break it down: If the given triangle is not a right triangle, you can break it down into two right triangles. Calculate the area of each right triangle separately and then add them together to get the total area.
4. Use trigonometry: If you are comfortable with trigonometric functions, you can use them to find the angles of the triangle. Once you have the angles, you can use the formula (1/2) * a * b * sin(C) to calculate the area, where a and b are the given side lengths and C is the angle between them.
By following these tips and tricks, you can efficiently calculate the area of a triangle with given side lengths. Practice these methods and soon you will become a master at solving these types of problems.
Mastering the art of finding the area of a triangle with two sides of lengths 5 and 13
Calculating the area of a triangle can be a challenging task, especially when given only two side lengths. However, with the right formula and techniques, it is possible to master this skill. In this article, we have explored the step-by-step process of finding the area of a triangle with side lengths of 5 and 13.
By understanding the concept of a base and height in triangle calculations, we were able to determine the length of the base using the given side lengths. Additionally, the Pythagorean theorem helped us determine the height of the triangle. By applying the formula for finding the area of a triangle using the base and height, we were able to calculate the area accurately.
Furthermore, we have discussed the real-life applications of finding the area of a triangle with given side lengths, highlighting its importance in various fields such as architecture and engineering. Additionally, we have provided some tips and tricks for efficiently calculating the area of a triangle.
By mastering the art of finding the area of a triangle with two sides of lengths 5 and 13, you will be equipped with a valuable skill that can be applied in various situations. So, practice and hone your skills, and you will become a pro in no time!
Frequently Asked Questions
Q: Why is it important to find the area of a triangle with given side lengths?
A: Finding the area of a triangle allows us to determine the amount of space it occupies. This is useful in various fields such as architecture, engineering, and geometry.
Q: What is the formula for calculating the area of a triangle?
A: The formula for calculating the area of a triangle is (base x height) / 2. This formula applies to all types of triangles, regardless of their side lengths.
Q: How do I calculate the length of the base using the given side lengths?
A: To calculate the length of the base, you need to know the lengths of the other two sides. By subtracting the length of one side from the sum of the other two sides, you can find the length of the base.
Q: How do I determine the height of the triangle using the Pythagorean theorem?
A: The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. By rearranging the formula, you can solve for the height of the triangle.
Q: What are some real-life applications of finding the area of a triangle with given side lengths?
A: Finding the area of a triangle is useful in various real-life scenarios. For example, architects use it to determine the amount of material needed to construct a roof with triangular sections. Engineers use it to calculate the load-bearing capacity of triangular trusses in bridges. Additionally, surveyors use it to measure the area of irregularly shaped plots of land.
About The Author

Wendy Lee is a pop culture ninja who knows all the latest trends and gossip. She's also an animal lover, and will be friends with any creature that crosses her path. Wendy is an expert writer and can tackle any subject with ease. But most of all, she loves to travel - and she's not afraid to evangelize about it to anyone who'll listen! Wendy enjoys all kinds of Asian food and cultures, and she considers herself a bit of a ninja when it comes to eating spicy foods.